Alternate Versions of the Cayley-Dickson Doubling Process

All the following presupposes that the basis vectors are defined recursively as given below, not for other methods of indexing.

1. \(e_{0}=1\)
2. \(\mathbf{e}_{2p}=(\mathbf{e}_p,0)\text{ for all } p\ge0\)
3. \(\mathbf{e}_{2p+1}=(0,\mathbf{e}_p)\text{ for all } p\ge0\)

Suppose multiplication is defined on elements of a ring \(K\) with identity \(1\) and suppose there is an involution \((^*)\) on \(K\) satisfying \((xy)^*=y^*x^*, (x+y)^*=x^*+y^*\) and a norm \(\lVert x\rVert\) satisfying \(\lVert x\rVert^2=xx^*=x^*x\).

A doubling product on \(K\times K\) is a product on ordered pairs of elements of \(K\) for which

1. \((1,0)\) is both a left and right identity
2. \((a,b)(a,b)^*=(\lVert a\rVert^2+\lVert b\rVert^2,0)=\Vert(a,b)\rVert^2\) where \((a,b)^*=(a^*,-b)\).

If \(K\) is the set of real numbers, then there are 32 possible products \((a,b)(c,d)\) satisfying the properties above. However, only eight of those products also satisfy the quaternion properties.

The basis vector products satisfy the quaternion properties if it is true that if \(\mathbf{e}_p\mathbf{e}_q=\mathbf{e}_r\) then it follows that \(\mathbf{e}_q\mathbf{e}_p=-\mathbf{e}_r\) and \(\mathbf{e}_q\mathbf{e}_r=\mathbf{e}_p\)

The eight products satisfying properties 1 and 2 above plus the quaternion properties are as follows:

• \(P_0\quad(a,b)(c,d)=(ca-b^*d,da^*+bc)\)
• \(P_1\quad(a,b)(c,d)=(ca-db^*,a^*d+cb)\)
• \(P_2\quad(a,b)(c,d)=(ac-b^*d,da^*+bc)\)
• \(P_3\quad(a,b)(c,d)=(ac-db^*,a^*d+cb)\)
• \(P_4\quad(a,b)(c,d)=(ca-bd^*,ad+c^*b)=P_0^T\)
• \(P_5\quad(a,b)(c,d)=(ca-d^*b,da+bc^*)=P_1^T\)
• \(P_6\quad(a,b)(c,d)=(ac-bd^*,ad+c^*b)=P_2^T\)
• \(P_7\quad(a,b)(c,d)=(ac-d^*b,da+bc^*)=P_3^T\)

The P₃ is the one more commonly used today, but its transpose P₇ is the one used by R. Shafer in his 1954 paper "On the algebras formed by the Cayley-Dickson process."

All eight of these products result in the imaginary i equaling e₁=0,1,0,0, . . .. For the first four, the quaternion j=e₂=0,0,1,0,0, . . . and k=e₃=0,0,0,1,0, . . . . For the last four, k=e₂and j=e₃.

Note: Four of these products fail to produce the octonions at the third doubling, P₁, P₂, and their transposes, so these four are not Cayley-Dickson doubling products.

If \(p, q \)and \(r\) are three distinct positive integers then the symbol \((p,q,r)\) means \(\mathbf{e}_p\mathbf{e}_q=\mathbf{e}_r\).

Because of the quaternion properties we have \((p,q,r)\to(q,r,p)\to(r,p,q)\).

These cycles can be used to create the multiplication tables for the basis elements.

The eight corresponding sets of cycles for the third doublings are

• \(P_0\quad(1,2,3),(1,4,5),(1,6,7),(2,6,4),(2,5,7),(3,4,7),(3,5,6)\)
• \(P_1\quad(1,2,3),(1,4,5),(1,6,7),(2,6,4),(2,7,5),(3,7,4),(3,6,5)\)
• \(P_2\quad(1,2,3),(1,4,5),(1,6,7),(2,4,6),(2,5,7),(3,4,7),(3,5,6)\)
• \(P_3\quad(1,2,3),(1,4,5),(1,6,7),(2,4,6),(2,7,5),(3,7,4),(3,6,5)\)
• \(P_4\quad(1,3,2),(1,5,4),(1,7,6),(2,4,6),(2,7,5),(3,7,4),(3,6,5)\)
• \(P_5\quad(1,3,2),(1,5,4),(1,7,6),(2,4,6),(2,5,7),(3,4,7),(3,5,6)\)
• \(P_6\quad(1,3,2),(1,5,4),(1,7,6),(2,6,4),(2,7,5),(3,7,4),(3,6,5)\)
• \(P_7\quad(1,3,2),(1,5,4),(1,7,6),(2,6,4),(2,5,7),(3,4,7),(3,5,6)\)

The Octonion Calculator is based on P₃.

Index Cycling

All eight of these doubling products satisfy a property called "index cycling."

For \(1\le p\le 7\) define the successor of \(p\) as the number \(p^\prime\) following \(p\) in the permutation \((1)(357)(246)\).

Then for each of these eight sets of quaternion cycles, \((p,q,r)\) implies \((p^\prime,q^\prime,r^\prime)\). This property is called index cycling

This is illustrated for \(P_0\) and \(P_7\)

\(P_0\quad(a,b)(c,d)=(ca-b^*d,da^*+bc)\)

Successor permutation: \((1)(357)(246)\)

• \((1,2,3)\to(1,4,5)\to(1,6,7)\to(1,2,3)\)
• \((2,6,4)\to(4,2,6)\to(6,4,2)\to(2,6,4)\)
• \((2,5,7)\to(4,7,3)\to(6,5,3)\to(2,5,7)\)

\(P_3^T\quad(a,b)(c,d)=(ca-bd^*,ad+c^*b)\)

Successor permutation: \((1)(357)(246)\)

• \((1,3,2)\to(1,5,4)\to(1,7,6)\to(1,3,2)\)
• \((2,4,6)\to(4,6,2)\to(6,2,4)\to(2,4,6)\)
• \((2,7,5)\to(4,3,7)\to(6,3,5)\to(2,5,7)\)

Some may complain that this is not really index cycling since we do not cycle through all seven states from any one given state. Point taken.

For \(P_0\quad(1,2,3),(1,4,5),(1,6,7),(2,6,4),(2,5,7),(3,4,7),(3,5,6)\) one may use the "successor" permutation \((1376524)\) to cycle through all seven states beginning with any one state.

Notice that the permutation \((1376524)\) may be recovered from the repeating binary sequence \([0011101]\) by 'sliding' a three bit window from left to right.

\((1,2,3)\to(3,4,7)\to(7,1,6)\to(6,3,5)\to(5,7,2)\to(2,6,4)\to(4,5,1)\to(1,2,3)\)

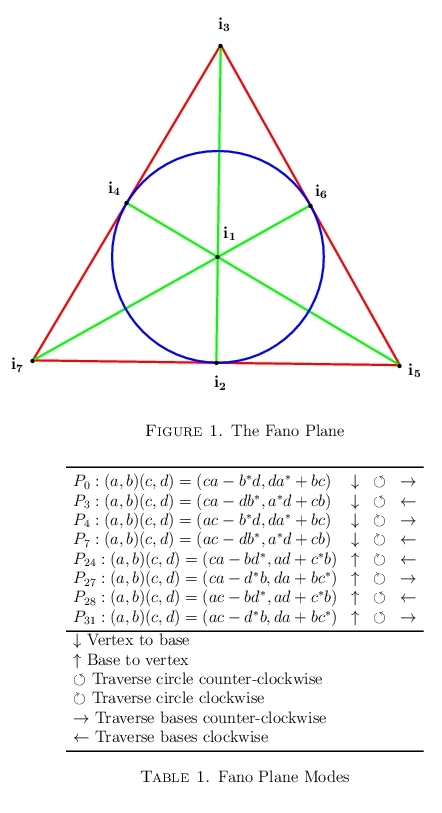
Diagram from "A catalog of Cayley-Dickson-like products" by J. W. Bales (2011); Dept. of Mathematics, Tuskegee University

The product numbering differs from that above as it is from the article in which the diagram appeared.

John W. Bales, Department of Mathematics (Retired 2015) Tuskegee University