An algebra of finite sequences
This is a development of a Cayley-Dickson algebra \(\mathbb{A}\) which contains all real Cayley-Dickson algebras as proper sub-algebras. The elements of \(\mathbb{A}\) consist of all sequences of real numbers which terminate in a string of
zeros (or, equivalently, all finite sequences of real numbers padded at the end by an unending string of zeros.)
Ordered pairs as shuffled sequences
An ordered pair of elements of \(\mathbb{A}\) will be represented by the shuffle of two sequences of \(\mathbb{A}\).
To illustrate: Given elements \( x=x_0,x_1,x_2,\cdots\) and \( y=y_0,y_1,y_2,\cdots\) of \(\mathbb{A}\), the ordered pair \( (x,y)\) represents the sequence \( x_0,y_0,x_1,y_1,x_2,y_2,\cdots\).
A real number \(x\) is represented by the sequence \(x,0,0,0\cdots\)
A complex number \( a+b\mathbf{i}\) is represented by the sequence \( a,b,0,0,0,\cdots\)
A quaternion \( a+b\mathbf{i}+c\mathbf{j}+d\mathbf{k}\) is represented by \( a,b,c,d,0,0,0\cdots\).
Notice that in this development of the elements of \(\mathbb{A}\), the quaternion \( a+b\mathbf{i}+c\mathbf{j}+d\mathbf{k}\) equals the ordered pair \( (a+c\mathbf{i}\,,\,b+d\mathbf{i}) = ((a,c),(b,d)) \).
Addition of two elements consists of adding corresponding elements of two sequences.
With this development we have that each ordered pair of elements of \(\mathbb{A}\) is an element of \(\mathbb{A}\) and each element of \(\mathbb{A}\) is a unique ordered pair of elements of \(\mathbb{A}\).
The canonical basis
A basis for \(\mathbb{A}\) consists of
\(\mathbf{e}_0=1,0,0,0,0,0,0\cdots\)
\(\mathbf{e}_1=0,1,0,0,0,0,0\cdots\)
\(\mathbf{e}_2=0,0,1,0,0,0,0\cdots\)
\(\mathbf{e}_3=0,0,0,1,0,0,0\cdots\)
\(\vdots\)
These satisfy the relations
-
\(\mathbf{e}_0=1\)
-
\(\mathbf{e}_{2r}=(\mathbf{e}_r,0)\)
-
\(\mathbf{e}_{2r+1}=(0,\mathbf{e}_r)\)
These relations follow from the "shuffle" process and will, accordingly, be
referred to as the "shuffle basis" for \(\mathbb{A}\).
An involution
In order that an involution on \(\mathbb{A}\) have the property \(x+x^*\in\mathbb{R}\) we define
\(x^*=x_0,-x_1,-x_2,-x_3,\cdots\)
From this definition it follows that for \(x, y\in\mathbb{A}\)
\((x,y)^*=(x^*,-y)\)
The sequence of Cayley-Dickson algebras
As a Cayley-Dickson algebra, we will consider the reals \(\mathbb{R}\) to be the set of all sequences \((x,0)\) for \(x\in\mathbb{R}\), and denote it by \(\mathbb{A}_0\).
There is a sequence of algebras \(\mathbb{A}_0\subseteq\mathbb{A}_1\subseteq\mathbb{A}_2\subseteq \cdots\subseteq\mathbb{A}_n\cdots\subset\mathbb{A}\) each of which is the set of ordered pairs of elements of the previous algebras in the
sequence and, as a result, each algebra \(\mathbb{A}_{n}\) has dimension \(2^n\).
\(\mathbb{A}_0\) is the set of real numbers
\(\mathbb{A}_1\) is the set of complex numbers
\(\mathbb{A}_2\) is the set of quaternions
\(\mathbb{A}_3\) is the set of octonions
\(\mathbb{A}_4\) is the set of sedenions
etc.
Doubling products
Regarded as ordered pairs of real numbers, complex numbers may be multiplied using the
doubling product
\((a,b)\cdot(c,d)=(ac-bd,ad+bc)\)
However, if we apply this same doubling product to ordered pairs of complex numbers, it will not produce the quaternions.
Given the shuffle basis, there are
eight
doubling products which produce the quaternions from ordered pairs of complex numbers. But only the four products listed below also produce the octonions from the quaternions.
Note that multiplication is commutative in \(\mathbb{A}_0\) and \(\mathbb{A}_1\) only, so the order of multiplication matters.
-
\(\mathbf{P}\phantom{^T}:\quad (a,b)\cdot(c,d)=(ac-db^*,a^*d+cb)\\ \)
-
\(\mathbf{P}^T:\quad (a,b)\cdot(c,d)=(ac-d^*b,da+bc^*)\\ \)
-
\(\mathbf{Q}\phantom{^T}:\quad (a,b)\cdot(c,d)=(ca-b^*d,da^*+bc)\\ \)
-
\(\mathbf{Q}^T:\quad (a,b)\cdot(c,d)=(ca-bd^*,ad+c^*b)\\ \)
One may experiment with product \(\mathbf{P}\) for the octonions using the
Octonion calculator
and for the sedenions using the Sedenion calculator.
These calculators use a level three
Reverse Polish
order of operations.
Multiplication of Basis Vectors
For the product \(\mathbf{P}:\quad (a,b)\cdot(c,d)=(ac-db^*,a^*d+cb)\\ \) the following multiplication tables are easily verified:
(Corner) block C of multiplication table:
\(\begin{array}{l|ll}
\mathbf{C} & \mathbf{e}_{0} & \phantom{-}\mathbf{e}_{1}\\
\hline \mathbf{e}_0 & \mathbf{e}_{0} & \phantom{-}\mathbf{e}_{1}\\
\mathbf{e}_1 & \mathbf{e}_{1} & -\mathbf{e}_{0}
\end{array}\)
(Top Row) block T: For all \(r>0\),
\(\begin{array}{l|ll}
\mathbf{T} & \mathbf{e}_{2r} & \phantom{-}\mathbf{e}_{2r+1}\\
\hline \mathbf{e}_0 & \mathbf{e}_{2r} & \phantom{-}\mathbf{e}_{2r+1}\\
\mathbf{e}_1 & \mathbf{e}_{2r+1} & -\mathbf{e}_{2r}
\end{array}\)
(Left Column) block L: For all \(r>0\),
\(\begin{array}{l|ll}
\mathbf{L} & \mathbf{e}_0 & \phantom{-}\mathbf{e}_1 \\
\hline \mathbf{e}_{2r} & \mathbf{e}_{2r} & -\mathbf{e}_{2r+1}\\
\mathbf{e}_{2r+1} & \mathbf{e}_{2r+1} & \phantom{-}\mathbf{e}_{2r}
\end{array}\)
(Diagonal) block \(-\)D: For \(r>0\),
\(\begin{array}{l|ll}
\mathbf{-D} & \mathbf{e}_{2r} & \phantom{-}\mathbf{e}_{2r+1}\\
\hline \mathbf{e}_{2r} & -\mathbf{e}_{0} & \phantom{-}\mathbf{e}_{1}\\
\mathbf{e}_{2r+1} & -\mathbf{e}_{1} & -\mathbf{e}_{0}
\end{array}\)
(INterior) block N: For \(0\ne r\ne s\ne0\), and \(r\oplus s=t\). [The operation \(\oplus\) is defined below.]
\(\begin{array}{l|ll}
\mathbf{N} & \mathbf{e}_{2s} & \phantom{-}\mathbf{e}_{2s+1}\\
\hline \mathbf{e}_{2r} & \phantom{-}\mathbf{e}_{2t} & -\mathbf{e}_{2t+1}\\
\mathbf{e}_{2r+1} & \mathbf{-e}_{2t+1} & \mathbf{-e}_{2t}
\end{array}\)
The corresponding tables for the product \(\mathbf{P}^T\) are the transposes of these tables.
This transpose relationship of the product tables holds for each of the products and its transpose.
Further along we will see the reason for \(-\)D as opposed to D.
The Cayley-Dickson Twist
As a result of the shuffle basis, the product of two basis elements satisfies the identity
\(\mathbf{e}_r\cdot\mathbf{e}_s=\omega(r,s)\mathbf{e}_{r\oplus s}\)
where \(r\oplus s\) is the 'exclusive or' operation on the binary representations of \(r\) and \(s\) and where \(\omega(r,s)\) maps ordered pairs of integers onto \(\{-1,1\}\).
The function \(\omega\) turns the Cayley-Dickson algebra \(\mathbb{A}\) into a
twisted group algebra .
By induction it can be shown that the \(\omega\) twist function for each \(\mathbb{A}_n\)satisfies the following properties:
-
\(\omega(p,0)=\omega(0,p)=1\\\) (using tables T, L)
-
\(\omega(p,p)=-1\) for \(p>0\\\) (using table D)
-
For \(0\ne p\ne q\ne0\\\) (using table N)
\(\begin{eqnarray}\omega(p,q)&=&\phantom{-}\omega(2p,2q)\\
&=&-\omega(2p,2q+1)\\ &=&-\omega(2p+1,2q)\\
&=&-\omega(2p+1,2q+1)\\ &=&-\omega(q,p)
\end{eqnarray}\)
The first two properties follow for all four of the doubling products. Property 3 varies for each of the four.
From Tables T and L, we see that doubling product \(P\) also satisfies the following two properties:
-
\(\omega(k,1)=(-1)^k\) for \(k>0\).
-
\(\omega(1,k)=(-1)^{k+1}\) for \(k>0\).
Building the twist tables from five elemental \(2\times2\) blocks
Note:
The rows and columns of all matrices will be numbered starting with row 0 and column 0
.
From each of the five elemental product tables we derive five
elemental twist blocks
:
-
\(\phantom{-}C=\left[\begin{array}{rr} 1 & 1\\
1 & -1 \end{array}\right]\)
-
\(\phantom{-}T=\left[\begin{array}{rr} 1 & 1\\
1 & -1 \end{array}\right]\)
-
\(\phantom{-}L=\left[\begin{array}{rr} 1 & -1\\
1 & 1 \end{array}\right]\)
-
\(-D=\left[\begin{array}{rr} -1 & 1\\
-1 & -1 \end{array}\right]\)
-
\(\phantom{-}N=\left[\begin{array}{rr} 1 & -1\\
-1 & -1 \end{array}\right]\)
Although \(C\) and \(T\) are the same we will soon see the reason for making a distinction.
The twist map for the quaternions \(\mathbb{H}=\mathbb{A}_2\) is
\(\left(\begin{array}{rr|rr}
1 & 1 & 1 & 1\\
1 &-1 & 1 &-1\\
\hline 1
&-1 &-1 & 1\\
1 & 1 &-1 &-1 \end{array}\right)
=\left(\begin{array}{rr}
C & T\\
L & -D
\end{array}\right)\) expressed in terms of the elemental twist blocks.
So, for example, \(\mathbf{e}_3\cdot\mathbf{e}_2=\omega(3,2)\mathbf{e}_{3\oplus2}=(-1)\mathbf{e}_1=-\mathbf{e}_1.\)
The twist map for the octonions \(\mathbb{O}=\mathbb{A}_3\) is
\(\left(\begin{array}{rr|rr|rr|rr}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\
1 &-1 & 1 &-1 & 1 &-1 & 1 &-1\\
\hline
1 &-1 &-1 & 1 & 1 &-1 &-1 & 1\\
1 & 1 &-1 &-1 &-1 &-1 & 1 & 1\\
\hline
&-1 &-1 & 1 &-1 & 1 & 1 &-1\\
1 & 1 & 1 & 1 &-1 &-1 &-1 &-1\\
\hline
1 &-1 & 1 &-1 &-1 & 1 &-1 & 1\\
1 & 1 &-1 &-1 & 1 & 1 &-1 &-1\\
\end{array}\right)
= \left(\begin{array}{r|r|r|r}
C & T & T & T\\
\hline L & -D & N & -N\\
\hline L & -N & -D & N\\
\hline L & N & -N & -D
\end{array}\right)\)
The first four tree components \(C,\,T,\,L,\,-D,\) are common to all four doubling products.
For each \(n>0\) the twist table for \(\mathbb{A}_{n+1}\) may be constructed by the following transformations on the twist tables for \(\mathbb{A}_{n}\):
\(\phantom{-}C\mapsto\left(\begin{array}{rr} \phantom{-}C & \phantom{-}T\\\phantom{-}L & -D \end{array}\right)\)
\(\phantom{-}T\mapsto\left(\begin{array}{rr} \phantom{-}T & \phantom{-}T\\\phantom{-}N & -N \end{array}\right)\)
\(\phantom{-}L\mapsto\left(\begin{array}{rr} \phantom{-}L & -N\\\phantom{-}L & \phantom{-}N \end{array}\right)\)
\(-D\mapsto\left(\begin{array}{rr} -D & \phantom{-}N\\-N & -D \end{array}\right)\)
\(\phantom{-}N\mapsto\left(\begin{array}{rr} \phantom{-}N & -N\\-N & \phantom{-}N \end{array}\right)\)
In order to generate the twist matrix for \(\mathbb{A}_4\), the sedenions, one applies these transformations to the corresponding twist matrix for the octonions.
Notice that although the elemental twist blocks for \(C\) and \(T\) are identical, they are transformed differently.
\(\left(\begin{array}{r|r|r|r} C & T & T & T\\
\hline L & -D & N & -N\\
\hline L & -N & -D & N\\
\hline L & N & -N & -D \end{array}\right)
\mapsto\left(\begin{array}{rr|rr|rr|rr}
C & T & T & T & T & T & T & T\\
L &-D & N &-N & N &-N & N &-N\\
\hline L &-N &-D & N & N &-N &-N & N\\
L & N &-N &-D &-N &-N & N & N\\
\hline L &-N &-N & N &-D & N & N &-N\\
L & N & N & N &-N &-D &-N &-N\\
\hline L &-N & N &-N &-N & N &-D &-N\\
L & N &-N &-N & N & N &-N &-D\\
\end{array}\right)\)
It should now be clear why the name chosen for the elemental twist block for the
diagonal block
was chosen to be \(-D\) rather than \(D\): By naming it in that manner, the signs of the twist matrix in twist block form for \(\mathbb{A}_{n+1}\) are the same as the signs in the twist matrix of \(\mathbb{A}_n\).
Binary indexing of binary order matrices
A matrix of size \(2^{n+1}\times2^{n+1}\) can be partitioned into a \(2\times2\) block matrix of sub-matrices of size \(2^{n}\times2^{n}\).
We will initially list subscipts in fractional form:
\(B=\left(\begin{array}{r|r} B_\frac{0}{0} & B_\frac{0}{1}\\\hline B_\frac{1}{0} & B_\frac{1}{1} \end{array}\right)\)
where the "numerator" is the block row number and the "denominator" is the block column number.
If the blocks are not of size \(1\times1\) we may further divide the matrix.
\(B=\left(\begin{array}{r|r}
B_\frac{0}{0} & B_\frac{0}{1}\\
\hline B_\frac{1}{0} & B_\frac{1}{1}
\end{array}\right)=
\left(\begin{array}{rr|rr} B_\frac{00}{00} & B_\frac{00}{01} & B_\frac{00}{10} & B_\frac{00}{11}\\
B_\frac{01}{00} & B_\frac{01}{01} & B_\frac{01}{10} & B_\frac{01}{11}\\
\hline B_\frac{10}{00} & B_\frac{10}{01} & B_\frac{10}{10} & B_\frac{10}{11}\\
B_\frac{11}{00} & B_\frac{11}{01} & B_\frac{11}{10} & B_\frac{11}{11} \end{array}\right)\)
Now, suppose that subdividing one more level results in single element entries:
\(\Large\left(\begin{array}{rr|rr|rr|rr}
b_\frac{000}{000} & b_\frac{000}{001} & b_\frac{000}{010} & b_\frac{000}{011} & b_\frac{000}{100} & b_\frac{000}{101} & b_\frac{000}{110} & b_\frac{000}{111}\\
b_\frac{001}{000} & b_\frac{001}{001} & b_\frac{001}{010} & b_\frac{001}{011} & b_\frac{001}{100} & b_\frac{001}{101} & b_\frac{001}{110} & b_\frac{001}{111}\\
\hline
b_\frac{010}{000} & b_\frac{010}{001} & b_\frac{010}{010} & b_\frac{010}{011} & b_\frac{010}{100} & b_\frac{010}{101} & b_\frac{010}{110} & b_\frac{010}{111}\\
b_\frac{011}{000} & b_\frac{011}{001} & b_\frac{011}{010} & b_\frac{011}{011} & b_\frac{011}{100} & b_\frac{011}{101} & b_\frac{011}{110} & b_\frac{011}{111}\\
\hline
b_\frac{100}{000} & b_\frac{100}{001} & b_\frac{100}{010} & b_\frac{100}{011} & b_\frac{100}{100} & b_\frac{100}{101} & b_\frac{100}{110} & b_\frac{100}{111}\\
b_\frac{101}{000} & b_\frac{101}{001} & b_\frac{101}{010} & b_\frac{101}{011} & b_\frac{101}{100} & b_\frac{110}{101} & b_\frac{110}{110} & b_\frac{110}{111}\\
\hline
b_\frac{000}{000} & b_\frac{000}{001} & b_\frac{000}{010} & b_\frac{000}{011} & b_\frac{110}{100} & b_\frac{110}{101} & b_\frac{110}{110} & b_\frac{110}{111}\\
b_\frac{111}{000} & b_\frac{111}{001} & b_\frac{111}{010} & b_\frac{111}{011} & b_\frac{111}{100} & b_\frac{111}{101} & b_\frac{111}{110} & b_\frac{111}{111}
\end{array}\right)\)
\(=\left(\begin{array}{ll|ll|ll|ll}
b_{0} & b_{1} & b_{4} & b_{5} & b_{16} & b_{17} & b_{20} & b_{21}\\
b_{2} & b_{3} & b_{6} & b_{7} & b_{18} & b_{19} & b_{22} & b_{23}\\
\hline
b_{8} & b_{9} & b_{12} & b_{13} & b_{24} & b_{25} & b_{28} & b_{29}\\
b_{10} & b_{11} & b_{14} & b_{15} & b_{26} & b_{27} & b_{30} & b_{31}\\
\hline
b_{32} & b_{33} & b_{36} & b_{37} & b_{48} & b_{49} & b_{52} & b_{53}\\
b_{34} & b_{35} & b_{38} & b_{39} & b_{50} & b_{51} & b_{54} & b_{55}\\
\hline
b_{40} & b_{41} & b_{44} & b_{45} & b_{56} & b_{57} & b_{60} & b_{61}\\
b_{42} & b_{42} & b_{46} & b_{47} & b_{58} & b_{59} & b_{62} & b_{63}
\end{array}\right)\)
Let us decode the subscripts of the second matrix. The binary form of the subscripts of the second matrix is found by shuffling the bits of the numerator and denominator of the subscripts of the first matrix. This may seem strange, but
there is a good reason for it.
For example, take \(b_{52}\). The index 52 in binary is 110100. The binary number results from shuffling row and column indices 100 and 110 (which are the numbers 4 and 6 in base 10). This indicates that element \(b_{52}\) occurs in row 4
column 6.
This strange way of indexing elements of a \(2^n\times2^n\) matrix leads to a simple way to evaluate the twist function \(\omega\) for ordered non-negative integer pairs \((r,s)\) using a
twist tree
.
Navigating the twist tree
For ease of presentation in a webpage, the tree is broken up into its components, with \(C\) being the root component.
The first four tree components \(C,\,T,\,L,\,-D,\) are common to all four doubling products, but the last two \(N,\,-N\) are particular to the standard doubling product \(P\). The other three doubling products have their own distinct values
for \(N,\,-N\).
In order to use the tree to find \(\omega(p,q)\) we express \(p\) and \(q\) in binary.
\(\mathbf{e}_5\cdot\mathbf{e}_6=\omega(5,6)e_{5\oplus6}=\omega(5,6)e_3\)
To find \(\omega(5,6)\) we shuffle the binary bits of \(5=101_B\) and \(6=110_B\) to get the bit string \(11,01,10\) (which have been grouped into pairs. These three binary pairs are instructions for moving through the tree, beginning at
\(C\).
A \(0\) is an instruction to move down a left branch and a \(1\) is an instruction to move down a right branch.
-
\(11:\quad \phantom{-}C\to-D\)
-
\(01:\quad -D\to \phantom{-}N\)
-
\(10:\quad \phantom{-}N\to-N\)
Arriving at either \(-N\) or \(-D\) indicates that \(\omega=-1\). Otherwise, \(\omega=1\).
Therefore \(\omega(5,6)=-1\). Thus \(\mathbf{e}_5\cdot\mathbf{e}_6=-\mathbf{e}_3\)

Therefore \(\omega(5,6)=-1\). Thus \(\mathbf{e}_5\cdot\mathbf{e}_6=-\mathbf{e}_3\)
Periodic properties of the twist
For non-negative integers \(p,\,q\), let \([p:\,q]\) denote a sequence of binary doublets consisting of the corresponding binary bits of \(p\) and \(q\).
For example, \([6:\,11]=[0110:\,1011]=01,10,11,01\).
The sequence \([p:\,q]\) is the path taken though the Cayley-Dickson tree to determine the value of \(\omega(p,q)\).
Since \([6:\,11]=01,10,11,01\longrightarrow T,N,-N,N\) we conclude that \(\omega(6,11)=1\).
THEOREM D: If \(2^{n-1}\le p < q < 2^n\) and if \(k\ge0\)
then \(\omega(p+k2^{n+1},q+k2^{n+1})=\omega(p,q)\).
PROOF: The binary representations of \(p\) and \(q\) each require exactly \(n\) bits, and the lead bit of each is \(1\). Thus \([p:\,q]=11,\cdots\).
The first doublet places us at \(-D\) in the tree, with the ultimate destination one of \(-D,\,-N\) or \(N\) depending upon the remaining binary doublets.
The first four tree components \(C,\,T,\,L,\,-D,\) are common to all four
Then \([p+k2^{n+1}:q+k2^{n+1}]=11,\cdots,[p:\,q]\) where the ellipsis is either empty or consists of a string of binary doublets \(11\) or \(00\).
Since an initial string of binary doublets \(11\) or \(00\) also leaves us at \(-D\), the result will be the same value of \(\omega\) as for \(p\) and \(q\).
So \(\omega(p+k2^{n+1},q+k2^{n+1})=\omega(p,q)\).
THEOREM T: If \(2^{n-1}< p< 2^n\le q < 2^{n+1}\) and if \(k\ge0\)
then \(\omega(p,q+k2^{n+1})=\omega(p,q)\).
\([p:\,q]=01,\cdots\) So the first doublet puts us at the \(T\) node of the tree.
\([p:\,q+k2^{n+1}]=01,\cdots,[p:\,q]\) The first doublet puts us at the \(T\) node. The ellipsis is either empty or a sequence consisting
of \(01\) or \(00\), both of which leave us at a \(T\) node.
So \(\omega(p,q+k2^{n+1})=\omega(p,q)\).
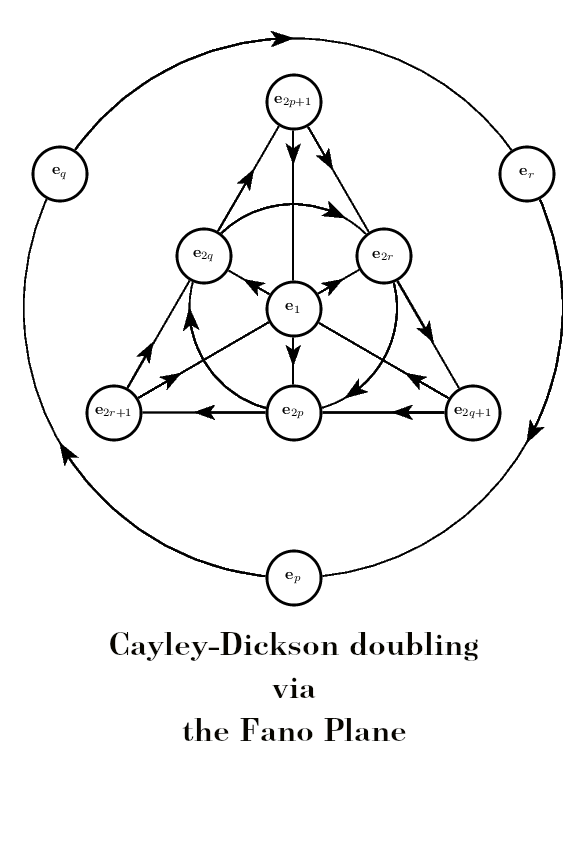
Properties of basis products
Let \(\mathbf{e}_0,\mathbf{e}_1,\cdots,\mathbf{e}_{2^n-1}\) denote the canonical basis vectors for the Cayley-Dickson algebra \(\mathbb{A}_n\).
The Cayley-Dickson product on \(\mathbb{A}_n\) follows from the product on the basis vectors according to the following properties:
- \(\mathbf{e}_0\) is the identity element
- \(\mathbf{e}_p^2=-\mathbf{e}_0\) for \(p>0\)
- For \(2p<2^n-1\) \(\mathbf{e}_1\mathbf{e}_{2p}=\mathbf{e}_{2p+1}\)
- If \(\mathbf{e}_p\mathbf{e}_q=\mathbf{e}_r\) then
- \(\mathbf{e}_q\mathbf{e}_p=-\mathbf{e}_r\)
- \(\mathbf{e}_q\mathbf{e}_r=\mathbf{e}_p\)
And if \(\mathrm{Max\{2p,2q,2r\}}<2^n-1\) then
- \(\mathbf{e}_{2p}\mathbf{e}_{2q}=\mathbf{e}_{2r}\)
- \(\mathbf{e}_{2q}\mathbf{e}_{2p+1}=\mathbf{e}_{2r+1}\)