9.2 Ellipses

The Geometric Definition

Given two points \(F_1\) and \(F_2\) in the plane lying a distance \(2c\) apart and given a distance \(2a > 2c\), the set of all points \(P\) whose distances to \(F_1\) and \(F_2\) respectively sum to \(2a\) is an ellipse. \(F_1\) and \(F_2\) are called the foci of the ellipse.

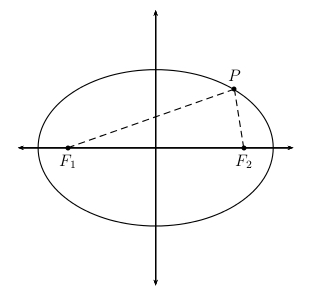
Exercise 9.2.1

Get a compass, the type for drawing circles, a straight edge and a blank sheet of paper.

On the sheet of paper, mark two points \(F_1\) and \(F_2\) as the foci and draw a dotted line through them.

Construct a dotted perpendicular line to \(F_1F_2\) through the midpoint of that segment.

Label the midpoint as the center.

Place the point of the compass at the center and open the compass to a fixed radius greater than the distance from the center to either focus.

Mark points \(V_1\) and \(V_2\) where the pencil of the compass crosses the line that passes through \(F_1\) and \(F_2\).

Without changing the radius on the compass, move the point of the compass to \(F_1\) and mark points \(V_3\)and \(V_4\) on the perpendicular that you constructed earlier.

Then the points \(V_1\), \(V_2\), \(V_3\), \(V_4\) are the vertices of an ellipse.

Draw a closed curve through the four points to represent the ellipse.

The line through the two foci is called the major axis, and the line through the center and perpendicular to the major axis is called the minor axis.

See Solution

Exercise 9.2.2

Using the ellipse that you drew in Exercise 9.2.1, denote the distance from the center to \(V_1\) and \(V_2\) as \(a\). Find the sum of the distances from \(V_1\) to \(F_1\) and \(V_1\) to \(F_2\) in terms of \(a\). Do the same for the sum of the distances from \(V_2\) to \(F_1\) and \(V_2\) to \(F_2\). Recall how the points \(V_3\) and \(V_4\) were constructed. Find the sum of the distances from \(V_3\) to \(F_1\) and \(V_3\) to \(F_2\) in terms of \(a\). Do the same for the sum of the distances from \(V_4\) to \(F_1\) and \(V_4\) to \(F_2\).

See Solution

Exercise 9.2.3

Let \(a\) denote the distance from the center to the major vertices \(V_1\) or \(V_2\) and let \(c\) denote the distance from the center to the foci \(F_1\) or \(F_2\).

Let \(b\) denote the distance from the center to the minor vertices \(V_3\) or \(V_4\).

Find an equation expressing the relationship between \(a, b\) and \(c\).

See Solution

Horizontal and Vertical Ellipses

We will consider only ellipses with either a vertical or a horizontal major axis.

Let us begin by considering a horizontal ellipse with center at the origin and foci \( (\pm c,0 )\) on the \(x\)-axis.

Let \(( \pm a, 0 )\) denote the major vertices and \(( 0, \pm b )\) the minor vertices.

The equation of this ‘horizontal’ ellipse is: \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)

If this ellipse is shifted h units horizontally and k units vertically, so that the center is at \(h,k)\) rather than \((0,0)\) the resulting ellipse will have equation: \(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\)

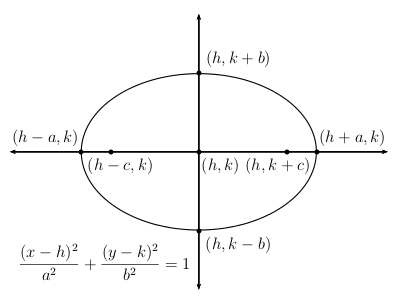
horizontal ellipse centered at origin

In either case \(c^2 = a^2 – b^2\).

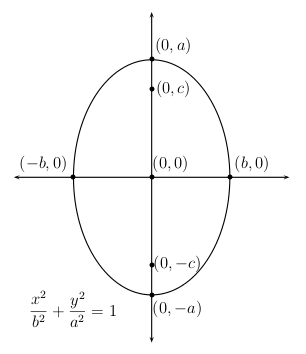
Next, consider an ellipse with a vertical major axis centered at the origin. Its major vertices are \(V_1=(0,a)\) and \(V_2=(0,-a)\) on the \(y\)-axis and its minor vertices are \(V_3=(b,0)\) and \(V_4=(-b,0)\) on the \(x\)-axis. Its foci are \(F_1=(0,c)\) and \(F_2=(0,-c)\) where \(c^2=a^2-b^2\). The equation of this verical ellipse is \(\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2}=1\).

vertical ellipse centered at origin

Notice that it is the case that \(a\) is always greater than \(b\). This allows one to determine from a glance at the equation whether the ellipse is horizontal or vertical: The graph of the equation \(\dfrac{x^2}{1}+\dfrac{y^2}{4}=1\) is a vertical ellipse because the larger denominator has numerator \(y^2\).

Exercise 9.2.4

Find the equation and sketch the graph of the ellipse with center ( 0, 0 ), focus ( -3, 0 ) and minor vertex ( 0, 4 ).

See Solution

Exercise 9.2.5

Find the equation and sketch the graph of the ellipse with center\( ( -2, 3 )\), focus\(( -3, 3 )\) and major vertex \(( 5, 3)\).

See Solution

Exercise 9.2.6

Find the equation and sketch the graph of the ellipse with center \(( 0, 0 )\), focus \(( 0, 2 )\) and major vertex \(( 0, -4 )\).

See Solution

Exercise 9.2.7

Find the equation and sketch the graph of the ellipse with center \(( 1, 3 )\), major vertex \(( 1, 0 )\) and minor vertex \(( 2, 3 )\).

See Solution

Completing the square and Standard Form

Be able to complete the square to put the equation of an ellipse in standard form. Be able to find the center, foci and vertices of an ellipse, given its equation.

For example, consider the equation:

\(x^2 + 9 y^2 – 2 x + 36 y + 28 = 0\)

To put this in standard form, we first separate the variables

\(x^2 – 2 x + 9 y2 + 36 y = - 28\)

Then we complete the squares on the two variables:

\((x^2 – 2 x + 1 ) + 9 (y^2 + 4 y + 4 ) = - 28 + 1 + 9 ( 4 )\)

\(( x – 1 )^2 + 9 ( y + 2 )^2 = 9\)

Then we divide by \(9\) to get

Thus, the ellipse is horizontal, \(a = 3\), \(b = 1\), and \(c=\sqrt{9-1}=2\sqrt{2}\).

The center is \(( 1, -2 )\), the major vertices are \(( 1 \pm 3, -2 )\) or \(( 4, -2 )\) and \(( -2, -2 )\). The minor vertices are \(( 1, -2 \pm 1 )\) or \(( 1, -3 )\) and \(( 1, -1 )\). The ellipse may be sketched through these four vertices. The foci are \((1\pm2\sqrt{2},-2)\).

Graph of horizontal ellipse, center=(1,-2), a=3, b=1

Exercise 9.2.8

Find the center, vertices and foci and sketch the graph of the ellipse with equation

\(25 x^2 + 9 y^2 – 50 x - 18 y - 191 = 0\)

See Solution