The Trigonometric Functions

4.2 The Trigonometric Functions

The trigonometric ratios

The six trigonometric functions are traditionally defined in terms of the six ratios of the sides of a right triangle. This approach is valid for positive angles of measure smaller than \(90^\circ\).

We will look at this traditional ratio approach first, then we will look at a method of defining the trigonometric functions for both positive and negative angles of any size.

Consider a right triangle \(\triangle ABC\) with the angle \(C\) being the \(90^\circ\) angle.

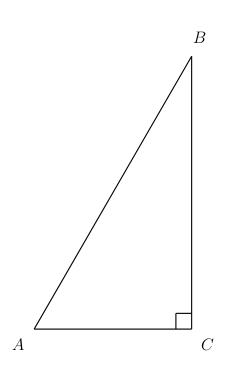
We will allow the letters \(A\), \(B\) and \(C\) do double duty. They will represent the vertices of the triangle, as well as the interior angles whose initial and terminal sides meet at that vertex.

Then we can define the six trigonometric functions of the angle \(A\) in terms of the six ratios of the triangle.

The sine function: \(\sin A = \dfrac{BC}{AB}=\dfrac{\text{opposite side}}{\text{hypotenuse}}\)

The cosine function: \(\cos A = \dfrac{AC}{AB}=\dfrac{\text{adjacent side}}{\text{hypotenuse}}\)

The tangent function: \(\tan A = \dfrac{BC}{AC}=\dfrac{\text{opposite side}}{\text{adjacent side}}= \dfrac{\sin A}{\cos A}\)

The cosecant function: \(\csc A = \dfrac{AB}{AC} = \dfrac{\text{hypotenuse}}{\text{opposite side}}=\dfrac{1}{\sin A}\)

The secant function: \(\sec A = \dfrac{AB}{AC}=\dfrac{\text{hypotenuse}}{\text{adjacent side}}= \dfrac{1}{\cos A}\)

The cotangent function: \(\cot A = \dfrac{AC}{BC}=\dfrac{\text{adjacent side}}{\text{opposite side}} = \dfrac{1}{\tan A} = \dfrac{\cos A}{\sin A}\)

Notice that the last three are the reciprocals of the first three and that the last four can be redefined in terms of the first two.

You will need to learn these relationships among the six functions.

There is a mnemonic or memory device students use to remember the first three of these: SOH CAH TOA

S = sine, C = cosine, T = tangent, O = opposite, H = hypotenuse, A = adjacent

Exercise 4.2.1

Suppose \(AC = 3\) and \(BC = 2\). Find all six trigonometric functions of \(\angle A\).

[Hint: You’ll have to use the Pythagorean Theorem to find the length of side \(AB\).]

Find all six trigonometric functions of \(\angle B\).

\(\angle B\) is called the complement of \(\angle A\), since any two positive angles which sum to \(90^\circ\) are called complementary angles.

How does \(\sin A\) compare to \(\cos B\)?

How does \(\tan A\) compare to \(\cot B\)?

How does \(\sec A\) compare to \(\csc B\)?

See Solution

Special \(45^\circ\) right triangle

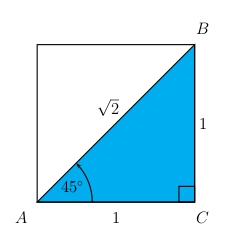
There is a special triangle which allows us to find the trigonometric functions of \(45^\circ\).

The right triangle with \(AC = 1\) and \(BC = 1\) is the part of the unit square lying below the diagonal \(AB\), with \(AB\) calculated using the Pythagorean theorem.

special forty-five degree right triangle

Exercise 4.2.2

Use the special triangle mentioned above to find all six trigonometric functions of the angle \(45^\circ\).

See Solution

Special \(30^\circ\) and \(60^\circ\) right triangle

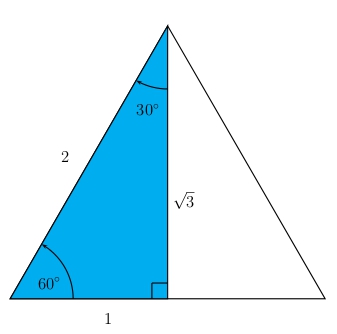
The right triangle with \(AC = 1\) and \(AB = 2\) is half of the equilateral triangle having all sides equal to \(2\). It can be used to find all six trigonometric functions of either \(60^\circ\) or \(30^\circ\).

Exercise 4.2.3

Use the special triangle to find all six trigonometric functions of \(60^\circ\)

See Solution

Exercise 4.2.4

Use the special triangle to find all six trigonometric functions of \(30^\circ\)

See Solution

Angles of any size or sign

Since we use angles to measure rotations, an angle can be of any size and can be positive in the case of a counter-clockwise rotation and negative in the case of a clockwise rotation. So far, we have seen only how to find the trigonometric functions of acute angles, that is, angles between \(0^\circ\) and \(90^\circ\) in size. Now we will see how to extend this to angles of any size or sign.

We will continue to use the geometry of the plane to find the trigonometric functions of an angle of any size or sign. We do so by placing the angle in standard position.

Every angle has an initial side representing the orientation at the beginning of the rotation and a terminal side, representing the orientation at the end of the rotation.

We place an angle in standard position by positioning the initial side to coincide with the positive \(\mathbf{x}\)-axis. Depending upon the size of the angle, its terminal side then will coincide with some ray or half-line originating from the origin, that is, from the point with coordinates \((0,0)\).

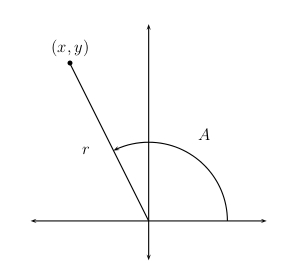
We pick any point \(( x, y )\) on the terminal side of the angle.

Let \(r\) denote the distance of the point \(( x, y )\) from the origin. Then \(r^2 = x^2 + y^2\)

The value of \(x\) or of \(y\) may be negative, but the value of \(r\) will never be negative.

Once the angle is in standard position, the six trigonometric functions may then be defined as follows:

The sine function: \(\sin A = y / r\)

The cosine function: \(\cos A = x / r\)

The tangent function: \(\tan A = y / x \)

The cosecant function: \(\csc A = r / y \)

The secant function: \(\sec A = r / x\)

The cotangent function: \(\cot A = x / y\)

Exercise 4.2.5

The terminal side of a standard angle \(A\) contains the point \(( -1,2 )\). Find all six trigonometric functions of the angle. You will have to find the value of \(r\) first.

See Solution

Trigonometric functions may sometimes have negative values

Did you notice that in this last exercise some of the six trigonometric functions had negative values and some had positive values. This is because \(x\) is negative and \(y\) is positive in the second quadrant.

There is a mnemonic for this: ALL STUDENTS TAKE CALCULUS

Of course, not all students take calculus, but this helps us to remember the following diagram of the four quadrants of the plane:

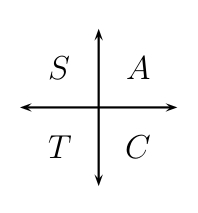
quadrants 1 through 4, All, Sine, Tangent, Cosine

The meaning is as follows:

In quadrant I all trigonometric functions are positive.
In quadrant II only the sine and its reciprocal are positive.
In quadrant III only the tangent and its reciprocal are positive.
In quadrant IV only the cosine and its reciprocal are positive.

Exercise 4.2.6

Determine the sign of \(x\) and \(y\) in each of the four quadrants.

Use the definitions of the six trigonometric functions (and the fact that \(r\) is never negative) to determine the sign of the six trigonometric functions in each of the four quadrants.

See Solution

quadrant angles

A quadrant angle is an angle in standard position whose terminal side lies on one of the axes

For example, \(0^\circ,90^\circ,180^\circ\) and \(270^\circ\) are quadrant angles. Others examples would be \(360^\circ, 450^\circ, -90^\circ, -180^\circ, -270^\circ\), etc. If a point \(P\) on the terminal side of a quadrant angle has coordinates \((x,y)\), then either \(x=0\) or \(y=0\). For this reason, some of the trigonometric functions of quadrant angles are undefined since division by zero is undefined.

Exercise 4.2.7

Use the points \((1,0), (0,1), (-1,0)\) and \((0,-1)\) as terminal points on \(0^\circ, 90^\circ, 180^\circ\), and \(270^\circ\) respectively in order to find all six trigonometric values of the angles.

Put the results into a table, indicating which trigonometric functions are undefined for which of the quadrant angles.

See Solution

A Pythagorean identity

The process of picking a point on the terminal side of an angle in standard position can be simplified if we agree to always pick the point exactly one unit from the origin so that \(r\) will always equal \(1\). In other words: Always pick \(( x, y )\) so that it lies on the unit circle. The unit circle is the circle centered at the origin with radius equal to one. When we pick the point of the terminal side lying on the unit circle we get an interesting and useful result:

If A is an angle in standard position crossing the unit circle at the point \(( x, y )\), then \(x = \cos A\) and \(y = \sin A\).

Since the equation of the unit circle is \(x^2 + y^2 = 1\), this implies another useful result:

\[ \cos^2A+\sin^2A = 1 \]

This is called a Pythagorean identity since it follows from the Pythagorean Theorem.

Note that \(\cos^2A\) means the same as \(\left(\cos A\right)^2\). When squaring a function, the '\(2\)' is always placed after the name of the function. So, for example, the square of \(f(x)\) is always written as \(f^2(x)\), never as \(f(x)^2\).

Exercise 4.2.8

Sketch the coordinate axes and the graph of the unit circle.
Draw an angle \(A\) in standard position and with terminal side in the first quadrant.
Draw the angle \(-A\) on the same diagram. Note the positions where \(A\) and \(-A\) cross the unit circle.
Label the point where the terminal side of \(A\) crosses the circle as \(( \cos A, \sin A )\) and the point where the terminal side of \(-A\) crosses the circle as \(( \cos ( - A ), \sin ( - A ) )\).
Can you guess the relationship between \(\cos ( - A )\) and \(\cos A\) ?
Between \(\sin ( - A )\) and \(\sin A\) ?
Recall that a function \(f\) is an odd function if \(f ( - x ) = - f ( x )\) and is even if \(f ( - x ) = f ( x )\).
Is the cosine function even or is it odd?
Is the sine function even or is it odd?
What about the tangent function? Use the fact that \(\tan A = \sin A /\cos A\) .

See Solution

Exercise 4.2.9

Sketch the coordinate axes and a large unit circle almost as wide as the sheet of paper. Use a compass to draw the circle.

Mark the four points where the axes cross the circle.

Without changing the radius of the compass, place the point of the compass at the point \((1,0)\) and mark a point on the circle in quadrant I and in quadrant IV with the pen of the compass.

Next, place the point of the compass at the point \((0,1)\) and mark points on the circle in quadrants I and II.

For each of the four points you marked on the circle with the pen of the compass, do the following:

Draw a line through the point and the center of the circle, continuing the line until it crosses the opposite side of the circle. When you have finished, the circle should be divided into 12 equal pie shaped wedges.

Now, beginning with the point \((1,0)\) and moving counterclockwise around the circle, label each of the twelve points with the angles from \(0^\circ\) to \(330^\circ\) in increments of \(30^\circ\).

Label the points a second time using radian measure.

See Solution

Exercise 4.2.10

Using the diagram you drew in exercise 4.2.9, label the coordinates of the points on the unit circle where the terminal sides of the quadrant angles cross. Next, label the coordinates of the points you drew on the circle in quadrant I. Then label the coordinates of all the remaining points on the circle using their symmetry with corresponding points in quadrant I. They will have the same coordinates of the points in quadrant I except that the signs of some coordinates will be different depending upon the quadrant. Remember \(x = \cos A\) and \(y = \sin A\). From this diagram you can immediately find the sine and cosine of any of the special angles which are multiples of \(30^\circ\). And using the \(x\) and \(y\) definitions of the other trigonometric functions, you can compute those values as well.

See Solution

Exercise 4.2.11

Sketch the coordinate axes and a large unit circle almost as wide as the sheet of paper. Use a compass to draw the circle. Draw the terminal side of the four quadrant angles together with the terminal sides of the angles \(45^\circ, 135^\circ, 225^\circ\) and \(315^\circ\). This should divide the circle into eight equal pie shaped wedges. Label the coordinates of each of these eight points. Recall that the coordinates of the point at the \(45^\circ\) mark equal \((\cos45^\circ,\sin45^\circ)\). Using this diagram you may find all the trigonometric functions of special angles which are multiples of \(45^\circ\).

See Solution

Exercise 4.2.12

Using a compass draw a large unit circle on a sheet of paper.
Draw the coordinate axes centered at the center of the circle.
Mark a point \(P\) on the circle in quadrant I and draw the terminal side of the angle \(A\) which crosses the circle at \(P\).
Draw a horizontal line through \(P\) until it intersects the circle in quadrant II. Label that intersection point \(P^\prime\).
Draw a vertical line through \(P^\prime\) until it crosses the circle in quadrant III. Label that point \(P^{\prime\prime}\).
Draw a horizontal line through \(P^{\prime\prime}\) until it crosses the circle in quadrant IV. Label that point \(P^{\prime\prime\prime}\).
Finally, draw a vertical line through the point \(P^{\prime\prime\prime}\).
If you were very careful, this last vertical line should cross the circle exactly at the original point \(P\), and you should have produced a rectangle through the four points.
Now draw the terminal sides of angles \(A^\prime, A^{\prime\prime}\), and \(A^{\prime\prime\prime}\) through the corners of the rectangle.
Label the coordinates of \(P\) as \(( x, y )\), the coordinates of \(P^\prime\) as \(( - x, y )\), the coordinates of \(P^{\prime\prime}\) as \(( - x, - y )\) and the coordinates of \(P^{\prime\prime\prime}\) as ( ? ).

See Solution

Reference angles

Notice the implication. The sine and cosine functions (and therefore all the trigonometric functions) of angles \(A^\prime, A^{\prime\prime}\), and \(A^{\prime\prime\prime}\) can be deduced from the corresponding sine and cosine functions of the acute angle \(A\). It will only be necessary to find the proper sign to affix, depending upon the quadrant in which the angle lies.

The rectangle you drew in exercise 4.2.12 is a reference rectangle for each of the angles passing through its vertices, and the angle \(A\) passing through the vertex in quadrant I is the reference angle of the angles \(A^\prime, A^{\prime\prime}\), and \(A^{\prime\prime\prime}\). The reference angle will always be between \(0^\circ\) and \(90^\circ\).

An alternate definition of the reference angle of an angle is the acute angle between the terminal side of the angle and the \(x\)-axis.

Exercise 4.2.13

Find the reference angle of each of the following angles:

\(112^\circ\)
\(195^\circ\)
\(295^\circ\)
\(395^\circ\)
\(-295^\circ\)

See Solution