Exercise 2.2.7
In order to complete the square, the coefficient of the \(x^2\) term must be one. If the coefficient is some other number besides one, that number must be factored out of both \(x\) terms.
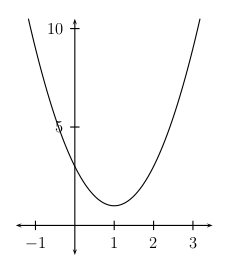
\(f ( x ) = 2x^2 - 4 x + 3\)
\(f ( x ) -3 = 2 ( x^2 - 2 x )\)
\(\dfrac{f ( x ) -3}{2} = x^2-2x\)
\(\dfrac{f ( x ) -3}{2} +1= x^2-2x+1\)
\(\dfrac{f ( x ) -3}{2} +1= (x-1)^2\)
\(f ( x ) -3+2= 2 ( x - 1 )^2\)
\(f ( x ) -1= 2 ( x - 1 )^2\)
\(f ( x ) = 2 ( x - 1 )^2\)+1
So the vertex is \(( 1, 1 )\). The graph is the same as the graph of \(y = 2 x^2\) shifted one unit right and one unit up.