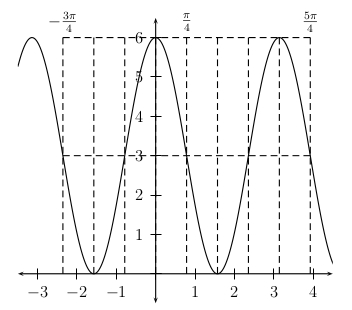
Exercise 4.4.5 solution
The amplitude is \(|-3|=3\), the vertical shift is \(3\), the period is \(\dfrac{2\pi}{2}=\pi\), the phase shift is \(\dfrac{\pi/2}{2}=\dfrac{\pi}{4}\).
Two cycles of \(y=\sin x\) would lie on the interval \([-2\pi,2\pi]\), therefore two cycles of \(y=-3\sin\left(2\pi-\frac{\pi}{2}\right)+3\) would lie on the interval which is the solution of the two part inequality \(-2\pi\le 2x-\frac{\pi}{2}\le 2\pi\).
The solution to this inequality is \(-\dfrac{3\pi}{4}\le x\le\dfrac{5\pi}{4}\).