Exercise 4.5.6 solution
If \(a\) is the height of the tree and \(b\) is the width of the river, then the situation may be diagramed as follows using right triangles:
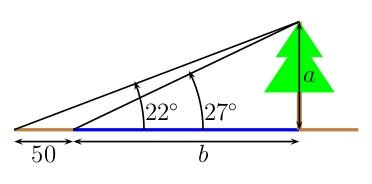
Then we may establish the following ratios.
\(\dfrac{a}{b}=\tan27^\circ\) and \(\dfrac{a}{b+50}=\tan22^\circ\)
Therfore, \(a=b\tan27^\circ\). Substituting this value for \(a\) into the second equation gives
\(\dfrac{b\tan27^\circ}{b+50}=\tan22^\circ\)
Solving for \(b\) gives \(b=\dfrac{50\tan22^\circ}{\tan27^\circ-\tan22^\circ}\approx191.5\) ft.