Exercise 4.5.7 solution
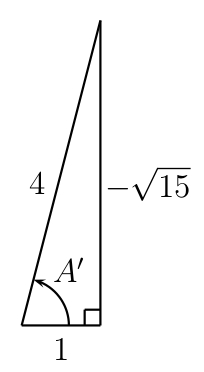
The secant equals the hypotenuse divided by the adjacent side, so we must label the sides of the triangle in such a way that that ratio equals 4. Since the angle in in quadrant IV where \(y\) is negative and \(x\) is positive, the adjacent side must be positive and the opposite side negative. Therefore, we may give the hypotenuse (which is never negative) a length of \(4\) and the adjacent side a length of \(1\). Then, using the Pythagorean theorem we must give a 'length' of \(-\sqrt{15}\) to the opposite side.
By reference to this triangle, we may easily find all six trigonometric ratios for angle \(A\).
- \(\sin A=-\dfrac{\sqrt{15}}{4} \)
- \(\cos A=\dfrac{1}{4} \)
- \(\tan A=-\dfrac{\sqrt{15}}{1}=-\sqrt{15} \)
- \(\csc A=-\dfrac{4}{\sqrt{15}}=-\dfrac{4\sqrt{15}}{15} \)
- \(\sec A=\dfrac{4}{1}=4 \)
- \(\cot A=-\dfrac{1}{\sqrt{15}}=-\dfrac{\sqrt{15}}{15} \)
The triangle above is an example of a 'pseudo-triangle' since one of its sides is negative. The angle \(A^\prime\) is actually the reference angle of the angle \(A\), but if we take into account that one or both sides (never the hypotenuse) may be negative then the trigonometric ratios of the reference angle will give the correctly signed value for the trigonometric values of \(A\) in the respective quadrant.
A pseudo-triangle is a right triangle in which the base angle \(A^\prime\) is the reference angle of \(A\), the adjacent side and the opposite side take the sign of the \(x\) and \(y\) coordinates, respectively, of points on the terminal side of \(A\) and the hypotenuse is always positive.
Pseudo-triangles are very useful for finding the correct trigonometric ratios for non-acute angles whose reference angles are acute.