Exercise 4.6.5 solution
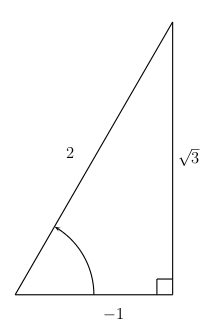
We want to find the tangent of the principle angle ( between \(0\) and \(\pi\) for secant ) whose secant is \(-2\) (so we are in quadrant II).
When labeling the triangle, the ratio of the hypotenuse to the adjacent side must be \(-2\). However, we cannot label the hypotenuse \(-2\), since the hypotenuse cannot be negative. We can put negative numbers on the adjacent and opposite sides, however, so we put \(+2\) on the hypotenuse and \(-1\) on the adjacent side.
The opposite side must be positive in quadrant II so its length is \(\sqrt{3}\).
The tangent of the angle will equal the opposite side divided by the adjacent side, so \(\tan\left(\sec^{-1}(-2)\right)=-\sqrt{3}\).