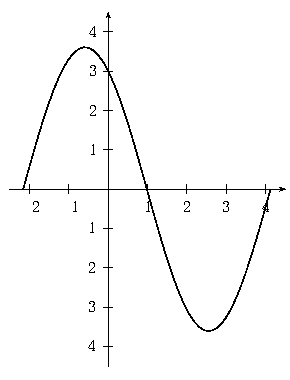
Exercise 5.3.5 solution
Factor out \(\sqrt{(-2)^2+3^2}=\sqrt{13}\) to get
\[ f(x)=\sqrt{13}\left[-\frac{2}{\sqrt{13}}\sin x+\frac{2}{\sqrt{13}}\cos x\right] \]Let \(\cos\phi=-\dfrac{2}{\sqrt{13}}\) and \(\sin\phi=\dfrac{3}{\sqrt{13}}\) then \(f(x)=\sqrt{13}[\cos\phi\sin x+\sin\phi\cos x]=\sqrt{13}\sin(x+\phi)\) where \(\phi=\arccos\left(-\dfrac{2}{\sqrt{13}}\right)\approx2.159\). Then the phase shift is \(-\phi=-2.159\). The amplitude is \(\sqrt{13}\) and the period is \(2\pi\).