Exercise 5.4.1 solution

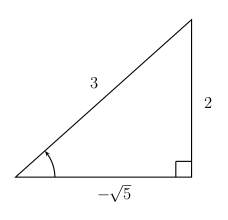
right triangle, opposite side=2, hypotenuse=3

In quadrant II, the \(x\) coordinate is negative, hence the adjacent side is \(-\sqrt{5}\).

\(\sin(2A)=2\sin A\cos A=2\left(\frac{2}{3}\right)\left(-\frac{\sqrt{5}}{3}\right)=-\frac{4\sqrt{5}}{9}\)

\(\cos 2A=\cos^2A-\sin^2A=\frac{5}{9}-\frac{4}{9}=\frac{1}{9}\)

Since \(\cos2A\) is positive and \(\sin2A\) is negative, the angle \(2A\) must lie in quadrant IV.