Exercise 5.5.1 solution
\(\cos x=0\)
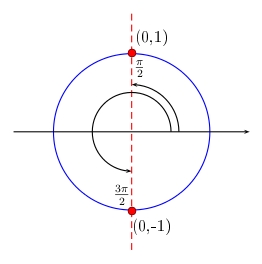
Draw the unit circle and draw a vertical line through \(0\) on the horizontal axis. The two points where this vertical lines crosses the unit circle represent the solutions to the equation, since every angle whose cosine is zero will have a terminal side which passes through one of these two points. The coordinates of these two points are \((0,1)\) and \((0,-1)\).
The two solutions in the interval \([0,2\pi)\) are \(\frac{\pi}{2}\) and \(\frac{3\pi}{2}\). Thus the general solution may be written as
\[ \theta=2\pi n+\frac{\pi}{2},2\pi n+\frac{3\pi}{2} \]
However, it can also be written more compactly as
\[ \theta=2\pi n\pm\frac{\pi}{2} \]