Exercise 5.5.2 solution
\(\sin A = -\frac{1}{2}\)
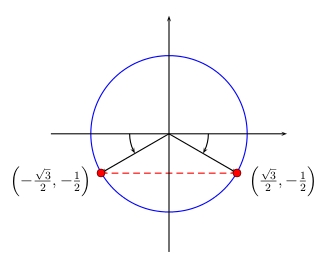
Draw the unit circle and draw a horizontal line crossing the \(y\)-axis at \(-\frac{1}{2}\).
The two points where the horizontal line crosses the unit circle represent the angles whose sines are equal to \(-\frac{1}{2}\) since their terminal sides cross the unit circle at those two points. These two points lie in quadrants III and IV.
The solution for \(\theta\) on the right half of the circle in quadrant IV is \(\arcsin\left(-\frac{1}{2}\right)=-\frac{\pi}{6}\) and the solution on the left half of the circle in quadrant III is \(\pi-\arcsin\left(-\frac{1}{2}\right)=\frac{7\pi}{6}\).
Therefore the set of all solutions is
\[ \theta=2\pi n-\frac{\pi}{6},2\pi n + \frac{7\pi}{6} \]