Exercise 5.5.3 solution
\(\sin\theta = 0.4\)
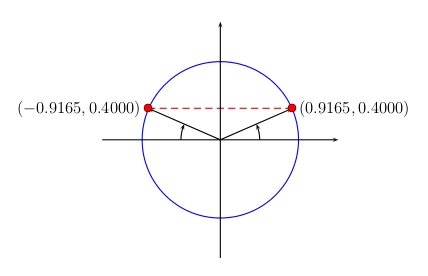
Draw the unit circle and draw a horizontal line through the number \(0.4\) on the \(y\)-axis.
The two points where this horizontal line crosses the unit circle represent the angles whose sines are \(0.4\), since their terminal sides must pass through one of these two points.
All the even multiples of \(\pi\) pass through the point \((1,0)\) and all the odd multiples of \(\pi\) pass through the point \((-1,0)\).
Thus the solutions lying in quadrant I are all the even multiples of \(\pi\) plus \(\arcsin (0.4)\) and all the solutions lying in quadrant II are all the odd multiples of \(\pi\) minus \(\arcsin (0.4)\). So the solutions are \(\theta = 2 n\pi + \arcsin(0.4), (2 n + 1)\pi – \arcsin(0.4)\)