Exercise 5.5.5 solution
\(\cos ( 3 x ) = \frac{1}{2}\) for \(0 \le x < 2\pi\). Since \(0 \le x < 2\pi\) it follows that \(0 \le 3x < 6\pi\).
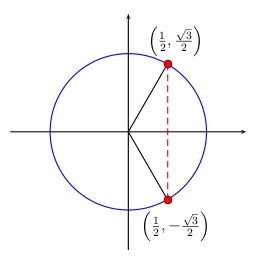
Draw the unit circle and draw the vertical line crossing the \(x\)-axis at \(\frac{1}{2}\).
The points where the vertical line crosses the unit circle are the points where the terminal sides of angles \(3 x\) cross the unit circle.
The angles \(3x=\frac{\pi}{3}\) and \(3x=\frac{5\pi}{3}\) are the only two values of \(3 x\) between \(0\) and \(2\pi\) satisfying \(\cos ( 3 x ) = \frac{1}{2}\). These correspond to solutions \(x = \frac{\pi}{9}\) and \(\frac{5\pi}{9}\).
But there are more solutions for \(x\) in the interval \([ 0, 2\pi) \).
To find all the solutions for for \(x\) in the interval \([ 0, 2\pi )\), we must find all the angles \(3 x\) in the interval \([ 0, 6\pi )\) for which \(\cos ( 3 x ) = \frac{1}{2}\).
So we move around the unit circle three times, that is, an angular distance of \(6\pi\) and note what the angle is each time we pass one of the two points where the \(x\)-coordinate is \(\frac{1}{2}\).
Those angles are are \(3x=\frac{\pi}{3},\frac{5\pi}{3}\), \(3x=\frac{\pi}{3}+2\pi,\frac{5\pi}{3}+2\pi\) and \(3x=\frac{\pi}{3}+4\pi,\frac{5\pi}{3}+4\pi\).
Divide these equations by \(3\) to get six solutions for \(x\) in the interval \([ 0, 2\pi )\), namely \(x = \dfrac{\pi}{9},\dfrac{5\pi}{9},\dfrac{7\pi}{9},\dfrac{11\pi}{9},\dfrac{13\pi}{9},\dfrac{17\pi}{9}\).