Exercise 6.4.4 solution

\(|u| = 3, | v | = 2, \theta = 45^\circ\)

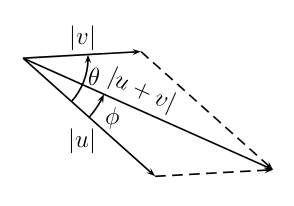
\(180^\circ - 45^\circ = 135^\circ\) is the angle of the triangle opposite the side representing the sum of the vectors

.

The angle opposite \(| v |\) is the angle between the vector \(u\) and the vector \(u + v\).

\(| u + v |^2 = | u |^2 + | v |^2 – 2 | u || v | \cos 135^\circ = 13+6\sqrt{2}\)

So, \(| u + v | = 4.635\)

Let \(\phi\) denote the angle between \(u\) and \(u + v\) . Then using the Law of Cosines

\(\cos\phi =\dfrac{|u|^2+|u+v|^2-|v|^2}{2|u|\cdot|u+v|}\approx0.9523\) so \(\phi\approx17.8^\circ\).

Copyright (c) 2012 John W. Bales. All rights reserved. Design (c) by FCT.