9.1 Parabolas

What is a parabola?

A parabola is a set of points in the plane that are equidistant from a given line, called the directrix and a given point not on the directrix, called the focus.

The point of the parabola lying halfway between the focus and the directrix is called the vertex. The number \(p\) will denote the distance from the vertex to the focus (or directrix).

If a line be drawn through the focus and parallel to the directrix, it will intersect the parabola at two points that lie a distance \(2p\) from the focus. The line segment connecting these two points is called the focal chord. The length of the focal chord is \(4p\).

The line drawn through the focus and the vertex is the axis of symmetry of the parabola.

Exercise 9.1.1

Draw a line on a sheet of paper and label it 'directrix'. Label a point that is not on the directrix as the focus. Plot the point lying exactly halfway between the focus and the directrix and label it 'vertex'. Draw the line through the focus and the vertex and label it 'axis of symmetry'. Draw the line through the focus and parallel to the directrix. Mark the two points on this line that are the same distance from the focus as the focus is from the directrix. You can use a compass to do this. Label the line connecting these two points 'focal chord'. The endpoints of the focal chord and the vertex are three of the points lying on the parabola. Sketch a curved line passing through these three points as a representation of the parabola.

See Solution

Horizontal Parabolas

We will consider only parabolas whose axes of symmetry are horizontal or vertical lines.

First, consider a parabola which has the \(x\)-axis for its axis of symmetry and focus \(( p, 0 )\). Then the directrix will be a vertical line crossing the \(x\)-axis at \(-p\). So the equation of the directrix is \(x = - p\). The equation of this parabola is

\[y^2 = 4 p x\]

When \(p > 0\), the focus is to the right of the vertex and the parabola opens to the right. When \(p < 0\), the parabola opens to the left.

If the parabola is shifted \(h\) units horizontally and \(k\) units vertically, its equation will be

\[( y - k )^2 = 4 p ( x - h )\]

Exercise 9.1.2

Sketch the graph of the parabola with vertex at \(( 0, 0 )\) and focus \(( 0, 2 )\).

Find the endpoints of the focal chord.

Write the equation of the parabola.

See Solution

Exercise 9.1.3

Sketch the graph of the parabola having focus \(( 1, 3 )\) and vertex \(( -1, 3 )\) by finding the endpoints of the focal chord.

Write the equation of the parabola.

See Solution

Vertical Parabolas

A parabola having the \(y\)-axis as its axis of symmetry and vertex at the origin, has focus at \(( 0, p )\) and directrix the line \(y = - p\). The equation of this parabola is

\[x^2 = 4 p y\]

If this parabola is shifted \(h\) units horizontally and \(k\) units vertically, the equation will be

\[( x - h )^2 = 4p ( y - k )\]

Exercise 9.1.4

Sketch the graph of the parabola having focus \(( 0, -2 )\) and vertex \(( 0, 0 )\) by first plotting the endpoints of the focal chord.

Write the equation of the parabola.

See Solution

Completing the square

Given the equation of a parabola, be able to put it into standard form by completing the square and be able to find the coordinates of its vertex, focus and the endpoints of the focal chord. Be able to find the equation of the directrix.

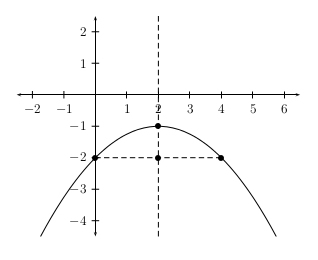
For example, consider the equation

\(x^2 – 4 x + 4 y + 8 = 0\)

Complete the square on the \(x\) terms to get

\[\begin{eqnarray*} ( x^2 – 4 x + 4 ) + 4 y + 8 &=& + 4\\ ( x – 2 )^2 &=& - 4 y – 4\\ ( x – 2 )^2 &=& - 4 ( y + 1 ) \end{eqnarray*}\]

Which is in standard form. We see that \(4 p = - 4\). Thus, \(p = - 1\). The vertex is at \(( 2, -1 )\) and the focus is \(–1\) units vertically from the vertex, thus the focus is at \(( 2, - 2 )\). The directrix will be the horizontal lying one unit above the vertex passing through the point \(( 2, 0 )\). Thus, the equation of the directrix is \(y = 0\). The endpoints of the focal chord lie a distance \(| 2 p |\) on either side of the focus, thus the endpoints of the focal chord are \(( 0, - 1 )\) and \(( 4, - 1 )\). A representation of the graph may be produced by drawing a curved line through the endpoints of the focal chord and the vertex.

Exercise 9.1.5

Complete the square to put the equation of the parabola into standard form. Find the coordinates of the vertex, focus, and the endpoints of the focal chord. Find the equation of the directrix.

\(y^2 + 4 y – 12 x + 40 = 0\)

See Solution