5.4 Multiple angle and half angle identities
Double angle identities
Since \(\sin ( A + B ) = \sin A \cos B + \cos A \sin B\), it follows from \(\sin(2A)=\sin(A+A)\) that
\(\sin ( 2A ) = 2 \sin A \cos A\)
which is the double angle identity for the sine function.
There are several double angle identities for the cosine function.
Since \(\cos ( A + B ) = \cos A \cos B - \sin A \sin B\), it follows from \(\cos(2A)=\cos(A+A)\) that
\(\cos ( 2A ) = \cos^2A - \sin^2A\)
and since \(\cos^2A = 1 - \sin^2A\) and \(\sin^2A = 1 - \cos^2A\), we get two additional identities
\(\cos ( 2A ) = 1 - 2 \sin^2A\)
and
\(\cos ( 2A ) = 2 \cos^2A - 1\).
Since \(\tan ( A + B ) = \dfrac{\tan A + \tan B}{1 - \tan A \tan B}\), it follows from from \(\tan(2A)=\tan(A+A)\) that
\(\tan ( 2A ) = \dfrac{2 \tan A}{1 - \tan^2A}\).
Exercise 5.4.1
Given that \(A\) is in quadrant II and \(\sin A = \frac{2}{3}\) find \(\sin ( 2A )\) and \(\cos ( 2A )\). In which quadrant does the angle \(2A\) lie?
Exercise 5.4.3
Given that \(A\) is in quadrant I and \(\cos A = \frac{3}{5}\), find \(\sin ( 3A )\). Hint: \(3A = A + 2A\)
Power reduction identities
The identities \(\cos2A= 1 - 2 \sin^2A\) and \(\cos2A = 2 \cos^2A - 1\) are sometimes written in the form
\(\sin^2A = \dfrac{1 - \cos2A}{2}\)
and
\(\cos^2A = \dfrac{1 + \cos2A}{2}\)
In this form, they are called the power reduction identities, since they reduce second powers of trigonometric functions to first powers of cosine functions.
In calculus there are simple rules for finding the anti-derivatives or Laplace transforms of functions of the form \(f(x)=\cos(ax)\). In order to apply those rules to finding antiderivatives or Laplace transforms of certain higher powers of sine or cosine, the power reduction identities are used.
For example,
\(\begin{eqnarray*} \cos^4x&=&\cos^2x\cdot\cos^2x\\ &=&\dfrac{1+\cos2x}{2}\cdot\dfrac{1+\cos2x}{2}\\ &=&\dfrac{1+2\cos2x+\cos^22x}{4}\\ &=&\frac{1}{4}+\frac{1}{2}\cos2x+\frac{1}{4}\cdot\dfrac{1+\cos4x}{2}\\ &=&\frac{3}{4}+\frac{1}{2}\cos2x+\frac{1}{8}\cos4x \end{eqnarray*} \)
Half-angle identities
If \(A\) is replaced by \(\dfrac{x}{2}\) in the power reduction identities and the resulting identities are solved for \(\sin\frac{x}{2}\) and \(\cos\frac{x}{2}\), then we get the half-angle identities for the sine and cosine functions.
\(\sin\frac{x}{2}=\pm\dfrac{\sqrt{1-\cos2x}}{2}\)
\(\cos\frac{x}{2}=\pm\dfrac{\sqrt{1+\cos2x}}{2}\)
For any particular angle \(x\) one would have to know which quadrant contains the angle \(\dfrac{x}{2}\) to decide whether the \(\pm\) becomes a plus \((+)\) or a minus \((-)\).
Exercise 5.4.4
Given that \(\dfrac{x}{2}\)is in quadrant II and \(\cos x = \frac{1}{2}\), find \(\cos\frac{x}{2}\) and \(\sin\frac{x}{2}\).
Tangent half-angle identities
In the unit circle, construct an angle \(A\) in standard position with its terminal side in quadrant I. Recall that the terminal side of \(A\) intersects the unit circle at the point with coordinates \((\cos A,\sin A)\). Construct a second angle \(B\) with its vertex at the point \(( -1, 0 )\), initial side the \(x\)-axis to the right of \(( -1, 0 )\) and terminal side containing the point \((\cos A,\sin A)\). Then, according to a theorem from geometry, \(B = \dfrac{A}{2}\).
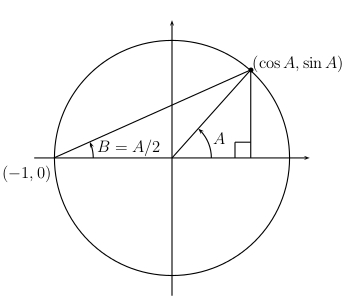
From the diagram we conclude that for acute angles \(A\)
\(\tan\frac{A}{2}=\dfrac{\sin A}{1+\cos A}\)
In fact, it is an identity for all angles \(A\), not only acute angles.
An equivalent identity is\(\tan\frac{A}{2}=\dfrac{1-\cos A}{\sin A}\)
We will leave this one as a puzzle for the student to work out. As a hint, draw the line between the points \((1,0)\) and the point \((\cos A,\sin A)\) and show that it is the hypotenuse of a small right triangle which is congruent to the large right triangle whose base angle is \(\frac{A}{2}\).
Exercise 5.4.5
Given that \(A\) is in quadrant IV and \(\cos A = \frac{4}{5}\), find \(\tan \frac{A}{2}\).