5.5 Solving Trigonometric Equations
The three basic types of trigonometric equations
In this section we will be using the greek letter \(\theta\) (theta) as the name of a general angle. It is common practice to use greek letters as angle names.
Before we can solve more general types of trigonometric equations, we must understand how to solve three basic types of trigonometric equations.
- \(\cos\theta=x\) where \(-1\le x\le 1\).
- \(\sin\theta=y\) where \(-1\le y\le 1\).
- \(\tan\theta=m\) where \(m\) is the slope of any line.
Equations of type \(\cos\theta=x\) where \(-1\le x\le 1\)
The cosine of an angle is always a number between \(-1\) and \(1\) inclusive. Thus an equation of the form \(\cos\theta=x\) has no solution unless \(-1\le x\le 1\).
Refer to the following diagram to understand what is involved in the process of solving \(\cos\theta=x\)
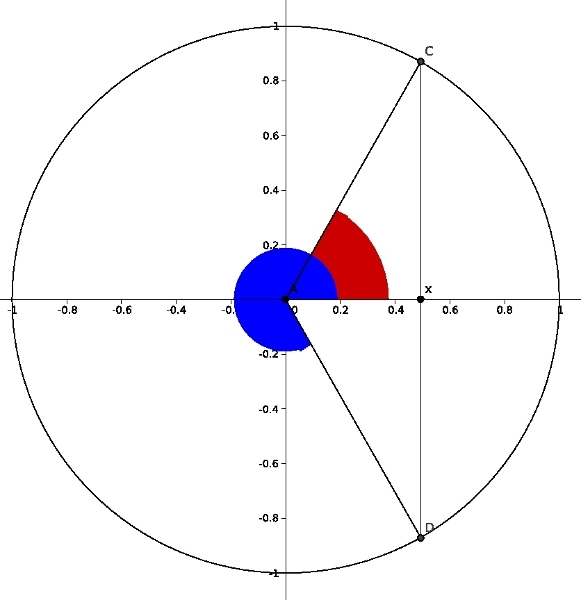
Any standard angle \(\theta\) whose cosine is \(x\) must have terminal side along either the segment \(AC\) or the segment \(AB\) in the diagram. This is because \(B\) and \(C\) are the only two points on the unit circle which have \(x\) as their first coordinate, and because of the fact that the first coordinate of the point where the terminal side of \(\theta\) intersects the unit circle is the cosine of \(\theta\).
There are an infinite number of solutions to the equation \(\cos\theta=x\). Only two solutions are shown in the diagram--the two solutions on the interval \([0,2\pi)\) (alternately, \([0^\circ,360^\circ)\)). But we can add or subtract any multiple to \(2\pi\) in radians (alternately \(360^\circ\)) to obtain as many additional solutions as necessary.
For example, to find all solutions to \(\cos\theta=\frac{1}{2}\) in the interval \([0,2\pi)\) one would draw a vertical line through the number \(\frac{1}{2}\) on the \(x\)-axis and identify the two angles in the interval \([0,2\pi)\) whose terminal sides crossed the unit circle at those two points of intersection. The angle on the upper half of the circle will always be \(\arccos x\)--in this case \(\arccos\left(\frac{1}{2}\right)\) which is \(\frac{\pi}{3}\) or \(60^\circ\). The solution in the lower half of the circle is always \(2\pi-\arccos\theta\) (alternately \(360^\circ-\arccos\theta\)). In this case the two solutions are \(\frac{\pi}{3}\) or \(\frac{5\pi}{3}\) (alternately, \(60^\circ\) or \(300^\circ\)). To represent all infinitely many solutions of \(\cos\theta=x\) we add any (positive or negative) whole number \(n\) multiples of \(2\pi\) (alternately, \(360^\circ\)) to these two solutions. Thus the set of all solutions may be written as
\[ \theta=2\pi n+\frac{\pi}{3},2\pi n+\frac{5\pi}{3} \]
alternately
\[ \theta=360^\circ n+60^\circ,360^\circ n+300^\circ \]
There are alternate ways to indicate all infinitely many solutions. For example, do you understand why the solution can also be written more compactly as follows?
\[\theta =2\pi n \pm\arccos x \]
Equations of type \(\sin\theta=y\) where \(-1\le y\le 1\)
The sine of an angle is always a number between \(-1\) and \(1\) inclusive. Thus an equation of the form \(\sin\theta=y\) has no solution unless \(-1\le y\le 1\).
Refer to the following diagram to understand what is involved in the process of solving \(\sin\theta=y\)
Any standard angle \(\theta\) whose sine is \(y\) must have terminal side along either the segment \(AC\) or the segment \(AD\) in the diagram. This is because \(D\) and \(C\) are the only two points on the unit circle which have \(y\) as their second coordinate, and because of the fact that the second coordinate of the point where the terminal side of \(\theta\) intersects the unit circle is the sine of \(\theta\).
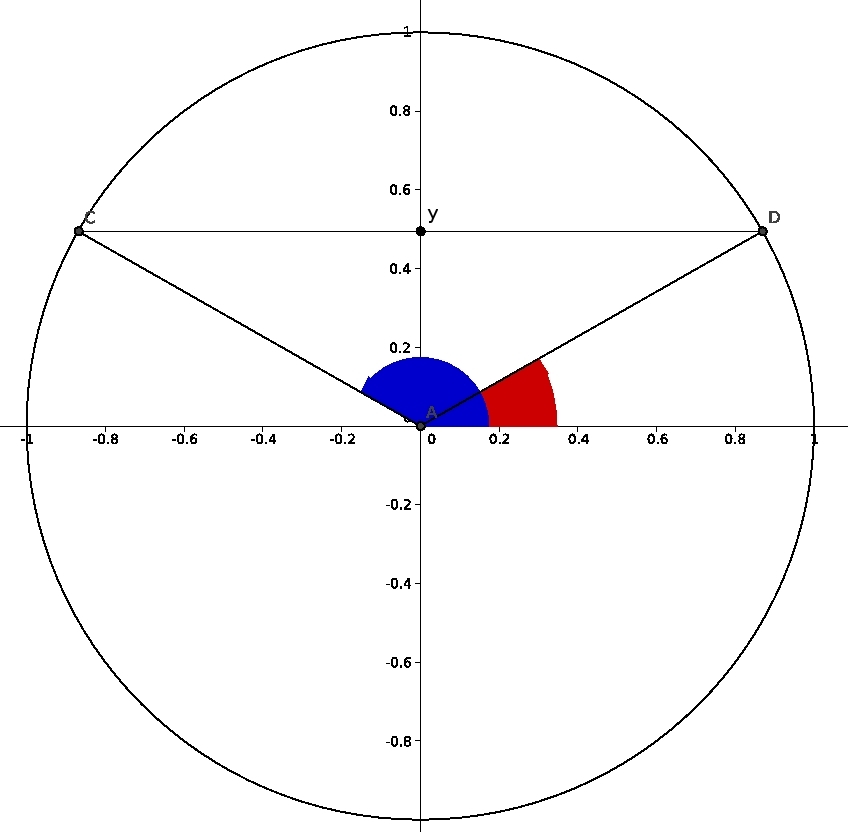
There are an infinite number of solutions to the equation \(\sin\theta=y\). Only two solutions are shown in the diagram--the two solutions on the interval \([0,2\pi)\) (alternately, \([0^\circ,360^\circ)\)). But we can add or subtract any multiple to \(2\pi\) in radians (alternately \(360^\circ\)) to obtain as many additional solutions as necessary.
For example, to find all solutions to \(\sin\theta=\frac{1}{2}\) in the interval \([0,2\pi)\) one would draw a horizontal line through the number \(\frac{1}{2}\) on the \(y\)-axis and identify the two angles in the interval \([0,2\pi)\) whose terminal sides crossed the unit circle at those two points of intersection. The angle on the right half of the circle will always be \(\arcsin y\)--in this case \(\arcsin\left(\frac{1}{2}\right)\) which is \(\frac{\pi}{6}\) or \(30^\circ\). The solution in the left half of the circle is always \(\pi-\arcsin\theta\) (alternately \(180^\circ-\arcsin\theta\)). In this case the two solutions are \(\frac{\pi}{6}\) or \(\frac{5\pi}{6}\) (alternately, \(30^\circ\) or \(150^\circ\)). To represent all infinitely many solutions of \(\sin\theta=y\) we add any (positive or negative) whole number \(n\) multiples of \(2\pi\) (alternately, \(360^\circ\)) to these two solutions. Thus the set of all solutions may be written as
\[ \theta=2\pi n+\frac{\pi}{6},2\pi n+\frac{5\pi}{6} \]
alternately
\[ \theta=360^\circ n+30^\circ,360^\circ n+150^\circ \]
Caveat: In the case where \(y < 0\), \(\theta=\arcsin y\) is also a negative angle in quadrant IV. If one wanted only positive solutions in the interval \([0,2\pi)\) they would have to be \(\pi-\arcsin y\) and \(2\pi +\arcsin y\).
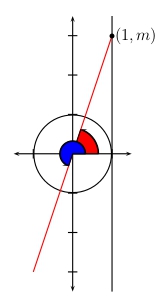
Equations of type \(\tan\theta=m\)
To solve \(\tan\phi = m\), construct the line through the origin having slope \(m\), with equation \(y = mx\). One way to relate this line to the unit circle is to construct a vertical line tangent to the unit circle at the point \((0,1)\) and mark the point \((1,m)\) on that vertical line as in the diagram. Note that if \(m\) is a negative number, then the point \((1,m)\) will lie in quadrant IV below the \(x\)-axis rather than in quadrant I. Every angle \(\theta\) in standard position whose terminal side is on the line \(y = mx\) is a solution to the equation \(\tan\theta =m\). In general the solution is \(\theta=\pi n+\arctan m\).
Exercise 5.5.4
Solve \(\sin^2A - \sin A = 0\). We're using \(A\) this time instead of \(\theta\) but that's OK. You will want to factor this first and set each factor to \(0\).
Equations involving multiple angles
Suppose we have to find all solutions of \(\sin2\theta=\frac{\sqrt{3}}{2}\) in the interval \([0,2\pi)\). We recognize \(\frac{\sqrt{3}}{2}\) as the sine of the special angle \(60^\circ\) or \(\frac{\pi}{3}\) so one solution is certainly found by solving \(2x=\frac{\pi}{3}\). That solution is \(\frac{\pi}{6}\). But to find all the solutions we have to analyze the problem as follows. If a solution \(\theta\) lies in the interval \([0,2\pi)\), then \(2\theta\) must lie in the interval \([0,4\pi)\). We draw the horizontal line through the points \(\left(\pm\frac{1}{2},\frac{\sqrt{3}}{2}\right)\) on the unit circle together with the line segments connecting those two points to the origin. Every angle \(2\theta\) in the interval \([0,4\pi)\) having one of those two segments as its terminal side is a solution for \(2\theta\). The solutions for \(2\theta\) in the interval \([0,4\pi)\) are \(2\theta=\frac{\pi}{3},\frac{2\pi}{3},\frac{7\pi}{3},\frac{8\pi}{3}\). Therefore the solutions for \(\theta\) in the interval \([0,2\pi)\) are \(\theta=\frac{\pi}{6},\frac{\pi}{3},\frac{7\pi}{6},\frac{4\pi}{3}\).
Exercise 5.5.5
Find all solutions in the interval interval \([0,2\pi)\) of the equation \(\cos ( 3 x ) = \frac{1}{2}\).