4.5 Applications of Right Triangle Trigonometry
Solving a side of a right triangle
When one knows one of the acute angles of a right triangle and the length of one of the sides, one can solve for the length of the other two sides using trigonometric functions of the given angle.
It is a convention that if a vertex of a triangle is denoted by an upper case letter, then the side opposite that vertex is denoted by the corresponding lower case letter. Thus the side opposite vertex \(A\) is \(a\), the side opposite \(B\) is \(b\), etc.
In the following examples, it will always be assumed that \(C\) is the right angle.
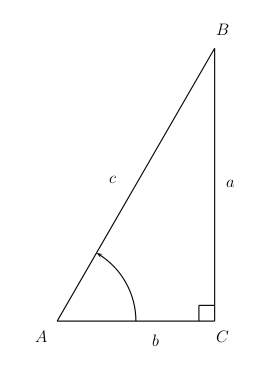
Example 1
Let \(A = 30^\circ\), and \(a = 10\). Find \(b\) and \(c\).
Form a ratio between the unknown side and the known side, with the known side in the denominator.
Determine which trigonometric function of the known angle represents that ratio, then equate the two.
To find \(c\), we solve \(\dfrac{c}{10} = \csc 30^\circ\). Thus, \(c = 10 \csc 30^\circ = 10(2) = 20\).
To find \(b\), we solve \(\dfrac{b}{10}= \cot 30^\circ\). Thus, \(b = 10\cot 30^\circ = 10\sqrt{3}\).
Exercise 4.5.2
Let \(A = 39.7^\circ\), and \(a = 3.46\). Find \(b\) and \(c\). Use a calculator. There is no \(\cot\) function on a calculator. You will have to use \(1\div\text{tan}\) instead. Likewise, you will have to use \(1\div\text{sin}\) instead of \(\csc\) since there is no cosecant function on a calculator.
See SolutionExercise 4.5.3
A flagpole stands in the middle of a flat, level field. Fifty feet away from its base a surveyor measures the angle to the top of the flagpole as \(48^\circ\). How tall is the flagpole?
See SolutionExercise 4.5.4
A 100 foot wharf sits along the bank of a river. A surveyor stands directly across the river from one end of the wharf. From where he stands the angle between the lines of sight to the two ends of the wharf is \(31^\circ\). How wide is the river?
See SolutionExercise 4.5.5
Standing across the street 50 feet from a building, the angle to the top of the building is \(40^\circ\). An antenna sits on the front edge of the roof of the building. The angle to the top of the antenna is \(52^\circ\). How tall is the building? How tall is the antenna itself, not including the height of the building?
See SolutionExercise 4.5.6
Standing on one bank of a river, an explorer measures the the angle to the top of a tree on the opposite bank to be \(27^\circ\). He backs up \(50\) feet and re-measures the angle to the top of the tree at \(22^\circ\). How wide is the river?
See SolutionThe Pythagorean Theorem and the Right Triangle Method
The famous Pythagorean Theorem of antiquity states that the sum of the areas of the two squares constructed on the sides of a right triangle equals the area of the square constructed on the hypotenuse. The hypotenuse is the side opposite the right angle.
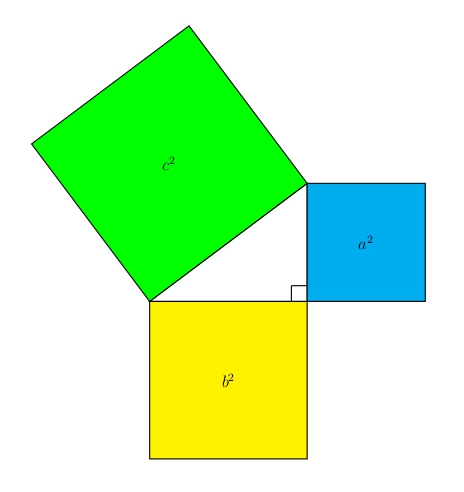
Applied to the right triangle depicted above, this principle can be expressed by the algebraic equation:
\[ a^2 + b^2 = c^2 \]
Given the value of one of the six trigonometric functions of an angle \(A\) and given the quadrant in which the terminal side of \(A\) lies when \(A\) is in standard position, the Right Triangle Method allows one to compute the values of the other five trigonometric functions of \(A\).
All that is needed is the basic definition of the six trigonometric functions, where we use \(x, y\) and \(r\) instead of \(a, b\) and \(c\). So \(x^2 + y^2 = r^2\).
Example 2
Given that angle \(A\) lies in quadrant II and\(\sin A = \frac{2}{3}\), draw and correctly label the sides of a right triangle in such a way that the other five trigonometric functions of \(A\) may be found using the basic definitions.
Solution: Draw a right triangle with base angle \(A\). Place a value of \(2\) on side \(a\) and a value of \(3\) on the hypotenuse. Using the Pythagorean Theorem, we write \(x^2 + 2^2 = 3^2\) and conclude that \(x^2 = 5\). So either \(x =\sqrt{5}\) or \(x = -\sqrt{5}\). But since \(A\) lies in quadrant II and since \(x\) coordinates in quadrant II are negative, it must be the case that \(x =-\sqrt{5}\).
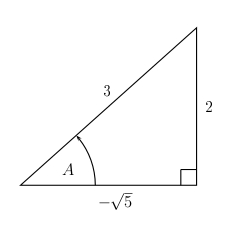
Now that all three sides are properly labeled, we can compute the other five trigonometric functions directly from the definitions.
But wait!! How can a triangle have a side with negative length? That is a valid question. The pseudo-triangle above (actual triangles cannot have negative sides) is actually the yellow triangle which appears in the figure below. And the angle labeled '\(A\)' in the triangle above is actually the reference angle of \(A\). But we can ignore all this and use the pseudo-triangle above and it will give us the correct values for all the trigonometric functions of \(A\).
One bit of caution, however: Even a pseudo-triangle cannot have a negative hypotenuse. The hypotenuse is always positive.
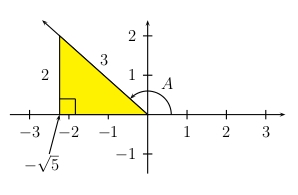
- \(\sin A=\dfrac{2}{3} \)
- \(\cos A=-\dfrac{\sqrt{5}}{3} \)
- \(\tan A=-\dfrac{2}{\sqrt{5}}=-\dfrac{2\sqrt{5}}{5} \)
- \(\csc A=\dfrac{3}{2} \)
- \(\sec A=-\dfrac{3}{\sqrt{5}}=-\dfrac{3\sqrt{5}}{5} \)
- \(\cot A=-\dfrac{\sqrt{5}}{2} \)
Example 3
\(\tan A = \frac{3}{4}\) and \(A\) is in quadrant III. Notice, that in quadrant III both \(x\) and \(y\) must be negative.
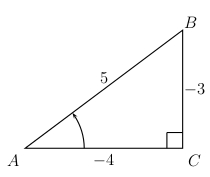
- \(\sin A=-\dfrac{3}{5} \)
- \(\cos A=-\dfrac{4}{5} \)
- \(\tan A=\dfrac{3}{4} \)
- \(\csc A=-\dfrac{5}{3} \)
- \(\sec A=-\dfrac{5}{4} \)
- \(\cot A=\dfrac{4}{3} \)
Exercise 4.5.7
Given that \(A\) is in quadrant IV and \(\sec A = 4\), correctly label the right triangle and use it to find the values of the other five trigonometric functions of \(A\).
See SolutionExercise 4.5.8
Given that \(A\) is in quadrant II and \(\cot A = t < 0\), find the other five trigonometric functions of \(A\) as functions of \(t\).
See Solution